Равнобедренный треугольник - это треугольник, у которого две стороны равны. Рассмотрим основные формулы и методы вычисления различных параметров такой фигуры.
Содержание
Основные свойства равнобедренного треугольника
- Две равные стороны называются боковыми
- Третья сторона - основание
- Углы при основании равны
- Высота, медиана и биссектриса, проведенные к основанию, совпадают
Формулы для вычисления параметров
| Параметр | Формула | Обозначения |
| Периметр | P = 2a + b | a - боковые стороны, b - основание |
| Площадь | S = (b/4) × √(4a² - b²) | a - боковые стороны, b - основание |
| Высота | h = √(a² - (b²/4)) | a - боковые стороны, b - основание |
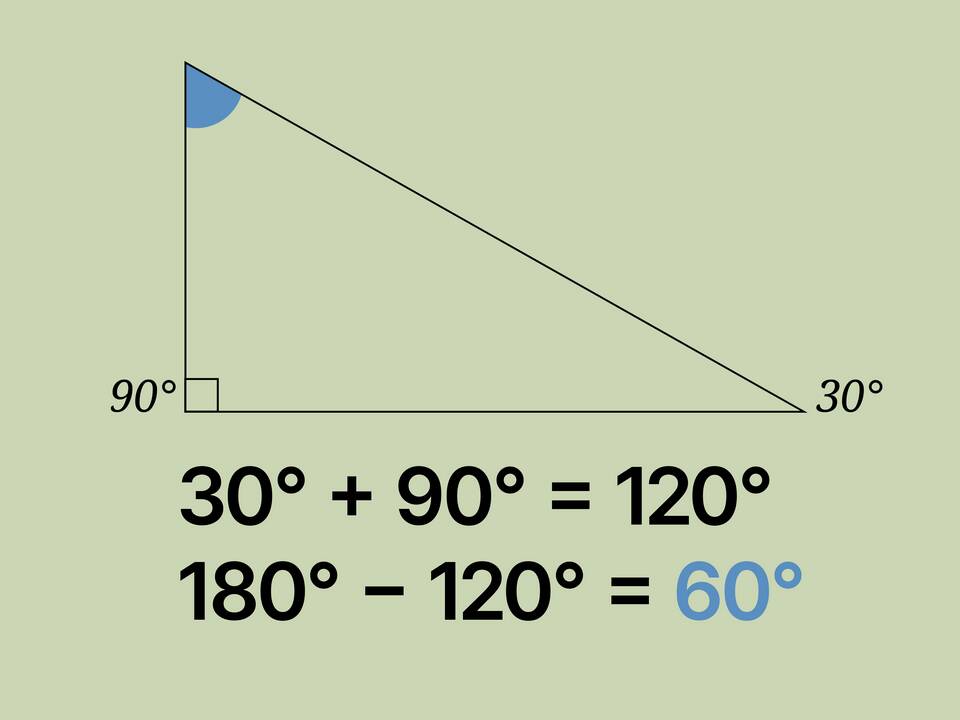
| Угол при вершине | α = 180° - 2β | β - угол при основании |
Пошаговые методы вычислений
Нахождение периметра
- Измерьте длину двух равных сторон (a)
- Измерьте длину основания (b)
- Подставьте значения в формулу P = 2a + b
Вычисление площади
- Способ 1: Через основание и высоту
S = (b × h)/2
- Способ 2: Через стороны (формула Герона)
S = √[p(p - a)(p - a)(p - b)]
где p = (2a + b)/2
Пример расчета
| Дано | Решение |
| Боковые стороны a = 5 см Основание b = 6 см | Периметр: P = 2×5 + 6 = 16 см Высота: h = √(5² - (6²/4)) = √(25 - 9) = 4 см Площадь: S = (6 × 4)/2 = 12 см² |
Особые случаи
Равносторонний треугольник
Является частным случаем равнобедренного, где все стороны равны. Все формулы упрощаются:
- P = 3a
- S = (a²√3)/4
- h = (a√3)/2
Прямоугольный равнобедренный треугольник
Угол при вершине равен 90°, боковые стороны - катеты:
- Основание (гипотенуза): b = a√2
- Площадь: S = a²/2